Формула расчета кредита

Расчет ежемесячного платежа по кредиту онлайн

Самый популярный и простой способ рассчитать размер ежемесячного платежа – воспользоваться онлайн калькулятором. Сегодня подобные простые и удобные сервисы размещены на официальных сайтах практически всех банков, а также многочисленных специализированных интернет ресурсах, посвященных вопросам кредитования и работы банковской системы страны. Обычно для выполнения расчета необходимо вбить в программу следующие данные, перечень которых может слегка изменяться в зависимости от вида займа:

• сумма и срок оформляемого займа;
• процентная ставка по кредиту;
• величина комиссий (при наличии таковых);
• размер первоначального взноса (если он планируется);
• дата начала погашения кредита;
• тип ежемесячных выплат (аннуитетные или дифференцированные).

Преимуществом использования онлайн калькуляторов, размещенных на сайтах различных банков, является наличие в базах их данных тарифов, установленных каждой конкретной кредитной организацией. Это существенно облегчает выполнение расчетов. Однако, при необходимости сравнения условий, предлагаемых различными банками, потребуется посетить несколько сайтов.

Важным плюсом использования онлайн калькуляторов является возможность оперативного выполнения множества расчетов, исходя из различных сроков кредитования или размера ежемесячного платежа. В результате потенциальный заемщик получает отличный шанс выбрать самый выгодный для себя вариант оформления займа.

Что может рассчитать онлайн-калькулятор Сбербанка

Для соискателей решающую роль при выборе банковского продукта играют три фактора:

1. Низкая процентная ставка.
2. Минимальный размер переплат.
3. Удобный график выплат.

Выполнить предварительные расчёты самостоятельно могут не все, поэтому онлайн-сервис крупнейшего банка РФ пользуется неизменной популярностью. Он позволяет частным лицам автоматически:

• рассчитать ежемесячный платёж;
• общую переплату;
• экономию при досрочном погашении;
• составить график погашения.

Диаграмма соотношения частей процентов и основного долга в ежемесячных выплатах поможет понять, как будет изменяться их структура на протяжении всего договора.

Переплата

Понятие включает в себя все расходы, которые предстоит понести клиенту, за исключением основного долга (ОД), то есть суммы кредита. Размер переплаты зависит от:

1. Суммы ОД.
2. Срока кредитования.
3. Процентной ставки.
4. Типа ежемесячных платежей.
5. Размера всех дополнительных комиссий (за услуги, обслуживание, страхование).

Достаточно ввести параметры в поля онлайн-калькулятора и расходы заёмщика станут очевидными. В Сбербанке переплата зависит только от процентной ставки. Дополнительные комиссии, скрытые платежи отсутствуют. Услуга страхования не является обязательной при подписании договора, но рекомендуется, чтобы клиент смог исполнить обязательства по договору даже в непредвиденной ситуации.

Формула расчета процентов по кредиту в Excel

Проведем расчет процентов по кредиту в Excel и вычислим эффективную процентную ставку, имея следующую информацию по предлагаемому банком кредиту:

Рассчитаем ежемесячную процентную ставку и платежи по кредиту:

Заполним таблицу вида:

Комиссия берется ежемесячно со всей суммы. Общий платеж по кредиту – это аннуитетный платеж плюс комиссия. Сумма основного долга и сумма процентов – составляющие части аннуитетного платежа.

Сумма основного долга = аннуитетный платеж – проценты.

Сумма процентов = остаток долга * месячную процентную ставку.

Остаток основного долга = остаток предыдущего периода – сумму основного долга в предыдущем периоде.

Опираясь на таблицу ежемесячных платежей, рассчитаем эффективную процентную ставку:

• взяли кредит 500 000 руб.;
• вернули в банк – 684 881,67 руб. (сумма всех платежей по кредиту);
• переплата составила 184 881, 67 руб.;
• процентная ставка – 184 881, 67 / 500 000 * 100, или 37%.
• Безобидная комиссия в 1 % обошлась кредитополучателю очень дорого.

Эффективная процентная ставка кредита без комиссии составит 13%. Подсчет ведется по той же схеме.

ПСК

Полная стоимость кредита — это и есть та самая величина, отражающая все затраты заемщика, которые он понесет в процессе уплаты основного долга по кредиту. Раньше эту информацию банк старался умалчивать, дабы клиент не передумал оформлять кредит. Однако, согласно закону от 2014 года, банк обязуется указывать эту сумму на первой странице кредитного договора и на обязательном графике платежей. Причем размер этой записи должен быть максимально большим, дабы избежать дальнейших недоразумений.

Рассчитать этот показатель можно по простой формуле:

ПСК=СК+СВК+%, где:

• СК — сумма кредита;
• СВК — сумма всех комиссий (разовых и ежемесячных);
• % — проценты по кредиту.

Дифференцированный платеж

Диф платеж предполагает неравномерные платежи, на уменьшение. В каждый платеж заложена:

• Фиксированная часть основного долга;
• Проценты на фактический остаток (так как с каждым месяцем остаток долга уменьшается, соответственно уменьшаются и проценты в составе платежа).

Пример: таблица расчета кредита с дифференцированным платежом:

Рассчитать дифференцированный платеж по кредиту также может калькулятор, встроенный на сайте банка, либо ценитель точных наук по формуле:

• Оставшуюся часть основного долга берем на каждую дату платежа.
• Число процентных периодов – количество месяцев до окончания кредита.
• Процентная ставка – эффективная годовая ставка.

Числа 100 и 12 в нашей формуле используются, чтобы перевести годовую ставку в проценты и определить проценты за 1 календарный месяц.

В формуле вы видите 2 части: одна из них постоянна, для каждого месяца (часть основного долга, которая ежемесячно снижает сумму задолженности). Например, если мы берем 12 тысяч рублей на 12 месяцев, то эта константа составит 1 тысячу рублей.

Переменная часть – проценты, зависит от остатка задолженности на конкретную дату. Эта сумма непостоянна, она уменьшается ежемесячно.

Если вас интересует, к примеру, как рассчитать кредит на 5 лет – да, придется сделать 60 расчетов, так как правильно рассчитать процент по кредиту можно только таким образом.

Что такое простой и сложный проценти чем они отличаются

Понятие простых и сложных процентов — один из самых важных уроков по финансовой грамотности, которые вы должны знать. Они встречаются в нашей жизни повсюду: от ежедневных покупок (кэшбек, бонусы) до инвестирования (проценты на депозит, дивиденды, комиссии и т.д.) и оказывают незаметное, но существенное влияние на ваш кошелек на длинной дистанции. Чтобы наглядно увидеть различия между простыми и сложными процентами, давайте рассмотрим примеры.

Допустим, вы открыли депозит 10000$ под 10% годовых, проценты начисляются раз в год. По схеме простого процента каждые 12 месяцев вы будете получать 1000$ прибыли, но она не остаётся на депозите и сразу же выводится. В итоге прирост прибыли будет выглядеть так:

Всё «просто» — каждый год плюс тысяча в карман. Простой процент используется в случаях, когда база начисления процентов не изменяется. Это могут быть специальные банковские депозиты, проценты по кредиту. Также простой процент используется, когда инвестор регулярно выводит прибыль — в каждый период времени работает первоначальная сумма.

Для сравнения пусть будет тот же депозит 10000$ под 10%, но банк в этот раз разрешает оставить прибыль на счёте. Вот что произойдёт с вкладом за 10 лет:

В первый год разницы нет — всё та же тысяча, но поскольку сумма на депозите теперь растёт, уже на втором году прибыль увеличивается: 2100$ вместо 2000$, за третий год 3310$ вместо 3000$ и так далее. За 10 лет доходность нашего депозита составила 159% вместо 100% когда мы выводили прибыль. Неплохая прибавка, не так ли? А вот что случится еще через несколько десятилетий:

Впечатляет! Чем дольше открыт депозит, тем сильнее работает эффект сложного процента — за 50 лет можно увеличить депозит не в 6, а более чем в 100 раз. Вот как это выглядит на графике:

без капитализации депозит растёт линейно, а с капитализацией — по экспоненте

Скачать график в Excel

Теперь киношные истории про забытые банковские счета, на которых накопились миллионы долларов выглядят вполне реальными 🙂 Конечно, 50 лет это много, но правило сложного процента неплохо работает и на более коротких промежутках времени — всё зависит от доходности вклада. Если хочется заработать больше, стоит использовать более прибыльные способы инвестирования: акции, драгоценные металлы, криптовалюты, валютный рынок и так далее.

Думаю, суть понятна, теперь давайте пройдемся по математической стороне вопроса, а потом рассмотрим несколько типичных примеров задач.

Пример использования сложных процентов

Далее выведем прибыльность сберегательного вклада с тем же условием, как и в предыдущем примере. Исключение составляет применение метода капитализированного процента.

Задача № 2

Условия депозита:

• Вложение — от 30 000 рублей.
• Депозитный срок — 6 месяцев (декабрь-май).
• Периодичность начисления и выплаты процентов — ежемесячно с капитализацией.
• Ставка по вкладу — 8,7 % годовых.

Алгоритм расчета приведен в таблице ниже.

Месяц	Сумма, рублей	Количество дней	Проценты	Итог по месяцам, рублей
1-й месяц	30 000	31	8,7 : (100 х 365)	221,67
2-й месяц	30 000 + 221,67	31	8,7 : (100 х 365)	223,31
3-й месяц	30 221,67 + 223,31	28	8,7 : (100 х 365)	203,19
4-й месяц	30 444,98 + 203,19	31	8,7 : (100 х 365)	226,46
5-й месяц	30 648,17 + 226,46	30	8,7 : (100 х 365)	220,77
6-й месяц	30 874,63 + 220,77	31	8,7 : (100 х 365)	229,77

В итоге спустя полгода сумма сложных процентов стала равной 1325,17 руб., итоговая сумма вклада с процентами — 31 325,17 руб. Таким образом, вклад с капитализацией процентов за 6 месяцев принес дополнительный доход в размере 30,87 руб.

Расчет годового процента по займу производился бы тем же путем. В ситуации взятия кредита или обращения в мелкие финансовые организации, такие как МФО, процентные начисления производятся таким же способом. Отличие заключается в формулировке названия. В случае депозита – это доходность, в случае кредита – это комиссии клиента или доходность самого банка.

Как посчитать годовую процентную ставку

Несмотря на кажущуюся сложность, формула расчета процентов по кредиту зависит от того, какой вид платежей вы используете для погашения кредита:

• Аннуитетный платеж – равный по сумме ежемесячный платеж, который состоит из основной суммы долга и начисленных на нее процентов. Как правило, такой вид платежей применяется в коммерческих кредитных организациях.
• Дифференцированный платеж – ежемесячная выплата по кредиту, которая уменьшается к концу срока кредита. В данный платеж также включен основной долг и сумма процентов на оставшуюся сумму.

Если вы получили кредит, то кредиторы ожидают, что вы выплатите им процент по займу за роскошь обладать суммой денег здесь и сейчас.

Это называется годовой процентной ставкой. Помните, что процентная ставка может быть рассчитана ежемесячно или ежедневно. Годовая процентная ставка – это ставка, которую вы платите по кредитам или займам.

Процентная ставка из процентов годовых I делением на 100 переводится в формат десятичной дроби. 2. Полученный результат делится на фактическое количество дней в году К — получаем процентную ставку за один день.

3. Процентная ставка за один день умножается на количество дней в расчетном периоде T — получаем ставку за конкретный период, например месяц. Это может быть не календарный месяц, а, например, период с 10.02.2014 по 09.03.2014.

Платежи и проценты по кредиту

Тип платежа соискатель выбирает сам, исходя из периодичности и размера личных финансовых поступлений. Аннуитетные и дифференцированные выплаты имеют существенные отличия, которые определяют их достоинства и недостатки.

Аннуитетный

Клиент совершает фиксированные ежемесячные взносы, первая часть которых идёт на погашение процентов по договору, вторая – уменьшает тело кредита. Проценты начисляются на фактическую сумму долга, а она с каждым периодом уменьшается, в последующих выплатах соотношение частей будет изменяться. При этом сумма основного платежа останется неизменной.

Кредитный калькулятор при выборе аннуитета по заданным соискателем параметрам рассчитывает:

1. Процентную ставку за платёжный период, чаще всего это 1 месяц (ПСМ). Вычисляется следующим образом: ПСГ/100/12 (количество месяцев в году).

1. Коэффициент аннуитета (КА) по формуле, где * — степень, равная общему количеству платежей:

ПСМ x (1 + ПСМ) *

(1 + ПСМ) * — 1

1. Сумму аннуитетного платежа (АП), которая равна: ОД x КА.

1. Проценты (СП) по формуле, где СЗ – размер фактической задолженности, которая в первом взносе всегда равна ОД: СЗ x ПСМ.

1. Их долю (ДСП): АП – СП.

1. Долю погашения ОД (ДОД): АП – ДСП.

Анализ расчётов, диаграммы и графика онлайн-сервиса Сбербанка покажет, что аннуитетный тип наиболее выгоден для финансового учреждения (переплата выше, чем при дифференцированном). Но он удобен для клиентов, которые получают стабильный фиксированный доход.

 Дифференцированный

На практике данный тип платежей применяется для ипотечных кредитов, но нередко банки используют его для потребительских программ. Главное отличие – стабильное уменьшение суммы ежемесячного платежа на протяжении всего срока действия договора. Основная финансовая нагрузка приходится на первые месяцы. Доля погашения ОД остаётся фиксированной для каждого периода, а размер процентов уменьшается.

Алгоритм расчёта параметров кредита с дифференцированным типом выплат для онлайн-калькулятора выглядит проще и состоит из вычислений:

1. Доли платежей, ежемесячно погашающих ОД – соотношение ОД и количества периодов срока кредитования (количество месяцев).
2. Доли процентов: произведение фактического ОД на ПСМ.
3. Размер дифференцированного платежа (ДП) для каждого периода: сумма доли процентов и ОД.

Проценты так же начисляются на остаток ОД, то есть их сумма становится меньше с каждым периодом.

Анализ результатов кредитного калькулятора покажет, что при строгом соблюдении графика выплат, дифференцированный тип предпочтительнее для некоторых клиентов, так как уменьшает переплату по продукту.

С помощью формул, соискатель может провести все расчёты по кредиту самостоятельно, но проще доверить эту работу кредитному калькулятору.

Как рассчитать долг на конец месяца в графике аннуитетных платежей

Прежде всего, надо понимать, что именно является вашим долгом по кредиту, и какие выплаты способствуют его уменьшению. В нашем примере вы берёте в кредит 50 000 рублей – это и есть ваш долг. Переплаченные по кредиту проценты (6157 рублей) вашим долгом не являются, это всего лишь вознаграждение банку за предоставленный кредит. Таким образом, можно сделать вывод:

Погашение процентов по кредиту никак не способствует уменьшению вашего долга перед банком.

В кризисные времена банки часто «идут навстречу» своим должникам. Они говорят как-то так: «Мы понимаем, у вас сейчас проблемы! Окей, наш банк готов пойти вам на уступки – можете нам просто погашать проценты, а само тело кредита погашать не надо. Все же люди братья и должны друг другу помогать! Бла-бла-бла…»

На первый взгляд такое предложение может показаться выгодным, а сам банк – «белым и пушистым лапулей». Ага, как бы ни так! Если взять в руки калькулятор и провести простые арифметические расчёты, то сразу становится ясно, что реальное предложение банка выглядит приблизительно так:

«Ребята, вы попали на деньги! Ничего не поделаешь, это жизнь! Предлагаем вам на время (а может и навсегда) стать нашим рабом – будете ежемесячно выплачивать проценты по кредиту, а сам долг погашать не надо (ну, чтобы сумма выплат по процентам не уменьшалась). Ничего личного – это просто бизнес, друзья!»

Теперь запомните главную мысль:

Именно погашение тела кредита вытаскивает вас из долговой ямы. Не процентов, а именно тела кредита.

Наверняка вы уже догадались, как рассчитывается долг на конец месяца в нашем графике платежей. В общем, формула выглядит так:

Обратите внимание! При расчёте долга на конец месяца, от общей суммы текущей задолженности отнимается только та часть платежа, которая идёт на погашение тела кредита (уплаченные проценты сюда не входят). Давайте для наглядности посчитаем, каким будет долг на конец месяца по нашему кредиту после внесения первого платежа:

Давайте для наглядности посчитаем, каким будет долг на конец месяца по нашему кредиту после внесения первого платежа:

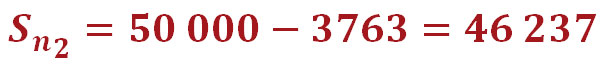
Итак, при первом платеже текущая задолженность по кредиту у нас равна всей сумме займа (50 000 руб.). Чтобы посчитать долг на конец месяца, мы отнимаем от этой суммы не весь ежемесячный платёж (4680 руб.), а только ту часть, которая ушла на погашение тела кредита (3763 руб.). В результате наш долг на конец месяца составит 46 237 руб., именно на эту сумму будут начисляться проценты в следующем месяце. Естественно, они будут меньше, так как сумма долга уменьшилась

Теперь вы понимаете, почему важно погашать именно тело кредита?

Итак, друзья, мы с вами разобрались с формулами и расчетами аннуитетных платежей. Надеемся, теперь у вас нет вопросов по этой теме, и вы запросто сможете произвести все необходимые расчеты, а также составить график аннуитетных платежей по кредиту. Единственное, что бы вам, наверное, хотелось, это как-то автоматизировать процесс расчетов. Вы не поверите, но это возможно! Хотите узнать как? Тогда переходим к публикации: Расчет аннуитетных платежей по кредиту в Excel.

Наши группы:

Формулы простых и сложных процентов

Поскольку простые и сложные проценты чаще всего используются при расчете прибыли от банковских вкладов, продолжим на их примере. Для решения задач нам понадобится такая информация:

• К — начальная сумма вклада;
• К — конечная сумма вклада;
• R — ставка доходности, переводится из процентов в число (10% = 0.1);
• N — количество периодов (лет).

Формула простого процента

По этой формуле мы можем рассчитать конечную сумму вклада без капитализации полученной прибыли. Для этого нужно знать начальную сумму вклада, процентную ставку за 1 период инвестирования и временной интервал. Если конечная сумма задана сразу и нужно найти другую неизвестную переменную, используйте производные формулы простого процента:

Формула сложного процента

По этой формуле мы можем посчитать конечную сумму вклада с учётом капитализации полученной прибыли, зная начальный депозит, процентную ставку и нужный временной интервал. Для решения задач также можно использовать производные формулы сложного процента:

На практике часто дело не заканчивается первоначальным депозитом — многие пользуются регулярными пополнениями, например делают регулярные инвестиции из зарплаты. Для этих случаев формула сложного процента становится длиннее:

где D — сумма регулярных пополнений банковского депозита

Обратите внимание, степень N-1 означает, что доливки начинаются со второго инвестиционного периода (если сумма дополнительных инвестиций вносится сразу, то N-1 меняется на N)

Ну что, удачи на экзаменах всем читающим меня студентам 🙂 Для закрепления далее мы разберем несколько примеров задач на сложные проценты.

Почему важно уметь рассчитывать проценты по своему кредиту

Многие россияне не могут позволить себе крупные покупки. Поэтому для приобретения бытовой техники или авто оформляют займы. Постепенное погашение долга позволяет безболезненно выполнить кредитные обязательства и получить необходимый товар.

Однако не всем удается погасить сумму займа успешно. Многие потребители до конца не понимают, какова реальная стоимость кредита, и как начисляются проценты по кредиту. Из-за этого не всегда могут вычислить размер ежемесячного взноса и выкроить такую сумму из своего бюджета. Как следствие — просрочки, испорченная кредитная история и долгие споры с кредитором.

Чтобы всего этого избежать, нужно знать, как рассчитать кредит и как вычислить процентную ставку. Существует две схемы, согласно которым рассчитывается стоимость кредита — аннуитетная и дифференцированная. Каждая из них имеет свою формулу просчета процента кредитования. Какая процентная ставка по кредиту выгодней и как посчитать сумму платежа, рассказано ниже.

Способы расчета

Гражданину стоит учесть, что итог самостоятельных вычислений может отличаться от суммы, получившейся у банка. Связано это с тем, что к выплатам прибавляют величину комиссии, расходы на оформление контракта, обязательную страховку. Их величины обязательно указывают в кредитном договоре. Рассчитать кредит можно следующими способами:

Способ расчета	Плюсы	Минусы
По формуле с составлением графика платежей вручную	Заемщик полностью поймет алгоритм подсчета процентов.	При необходимости внести изменения в график придется полностью переделывать все вычисления. При составлении графика платежей вручную велика вероятность допустить ошибку в расчетах, не учесть какую-либо величину. Вычисления вручную занимают много времени.
С помощью электронных таблиц Excel	Автоматический расчет по датам. При необходимости можно скорректировать формулу с учетом досрочного погашения, изменения процентной ставки и т.д.	Необходимо хорошо изучить функционал Excel.
Онлайн-калькулятором	Автоматический расчет.	Вычисления часто осуществляются без учета суммы комиссий и страхования. Календарь платежей придется оформлять в отдельном документе самостоятельно.

Переплата и дополнительные платежи

При получении кредита в банке есть ряд дополнительных платежей.
Для ипотеки:

1. страховка титула и имущества
2. расходы на оформление бумаг, договора долевого участия
3. оценку недвижимости,
4. Расходы на нотариуса
5. госпошлина в регистрационной палат

Для автокредита:

1. страхование транспортного средства — КАСКО и ОСАГО
2. пошлина за регистрацию транспортного средства

Нужно иметь ввиду, что данные расходы увеличивают переплату по кредиту. Обычно они добавляются к процентам по займу от банка.
Настоящей проблемой является подключение заемщиков к страхованию потребительских кредитов. Обычно при выдаче займа банк навязывает страховку.

Как рассчитать платеж при аннуитетном варианте расчета?

Основной способ оплаты долга, который в последнее время предлагают банки, – это аннуитетный платеж. То есть деньги возвращаются в банк равными долями в течение всего срока кредитования, причем большая часть идет на погашение процентов.

Данный вариант очень выгоден банку, поскольку кредитор гарантированно получает свои проценты, в то время как основной долг долгое время не уменьшается. То есть в случае досрочного погашения ссуды долг все еще будет немаленьким.

Формула расчета в этом случае выглядит следующим образом:

МП = К (П + (П/(1+П)ДК — 1)), где

• МП – месячный платеж по ссуде;
• К – основной долг;
• П – 1/12 от годовой процентной ставки по ссуде;
• ДК – срок возврата ссуды в месяцах.

Расчёт аннуитетного платежа по кредиту

Допустим, вы решили взять в кредит 50 000 рублей на 12 месяцев под 22% годовых. Естественно, тип погашения будет аннуитетный. Вам надо рассчитать сумму ежемесячных взносов по кредиту.

Давайте для начала красиво оформим наши исходные данные (они нам понадобятся не только в этом, но и в дальнейших расчетах):

Сумма кредита: 50 000 руб.
Годовая процентная ставка: 22%.
Срок кредитования: 12 месяцев.

Итак, прежде чем приступить к расчёту аннуитетного платежа, надо посчитать ежемесячную процентную ставку (в формуле она скрывается под символом i и рассчитывается так: годовая процентная ставка/100/12). В нашем случае получится следующее:

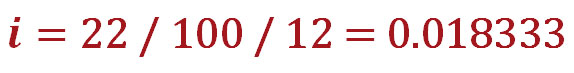
Теперь, когда мы нашли значение i, можно приступать к расчёту размера аннуитетного платежа по нашему кредиту:

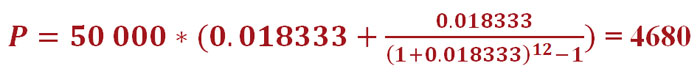
Путём несложных математических вычислений выяснилось, что сумма ежемесячных отчислений по нашему кредиту будет равна 4680 рублей.

В принципе, на этом можно было бы закончить нашу статью, но вы же наверняка хотите знать больше. Правда? Вот скажите, вы хотите знать, какую долю в данных выплатах составляют проценты по кредиту, а какую – тело кредита? Да и вообще, сколько вы переплатите по кредиту? Если да, тогда мы продолжаем!

Основные правила

Кредитор имеет право взимать со своего заёмщика плату за пользование средствами. Такая плата начисляется в виде процентов. Они указываются в договоре.

Если в договоре нет прямого указания на размер процентов, то они будут взиматься согласно ключевой ставке ЦБ РФ на день уплаты долга. Договор и сам займ будут считаться беспроцентными, если в соглашении так и будет написано.

Чтобы стороны были уверены в правильности расчётов по кредиту, им необходимо знать, как эти проценты рассчитываются. Это необходимо для того, чтобы избежать дальнейших спорных ситуаций, которые могут привести стороны в суд.

Чтобы самостоятельно рассчитать сумму процентов к уплате и конечный итог по кредиту, необходимо опираться на следующую информацию, указанную в договоре и в сопутствующих документах.

Это:

Точная сумма	которая выделена заёмщику в пользование
Размер процентов	которые взимаются за определённый период пользования. Не запрещается устанавливать проценты за месяц пользования средствами, квартал или год
Срок, на который выдан займ	он также может быть выдан на определённое количество дней, месяцев, кварталов или лет
Точное количество дней	в каждом месяце, квартале или году

Все эти сведения указываются в самом договоре или в дополнительном соглашении к нему.
Стороны могут договориться, чтобы кредит был возвращён единоразово, в конце срока заимствования, или же частями, по истечении определённого периода, то есть, аннуитетно.

О чем говорят законодательные акты

Если кредитор требует уплаты необоснованно высоких процентов, то клиент имеет право требовать их снижения.

Видео: потребительский кредит сколько переплачиваем

Какие составляющие формулы

Чтобы правильно самостоятельно рассчитать сумму процентов к уплате по договору займа, можно:

Воспользоваться онлайн-сервисами	на которых представлен калькулятор для расчёта процентов. Клиенту только остаётся ввести сумму, срок кредитования и проценты по договору. Система сама произведёт расчёт за считанные секунды
Самостоятельно их рассчитать	воспользовавшись специальными формулами

Чтобы быть до конца уверенным в правильности расчётов, нужно самостоятельно применить существующие формулы. Доверять онлайн-сервисам для того, чтобы рассчитать проценты по займу онлайн, не стоит! Они могут выдать ошибку.

Сначала рассчитываем проценты по договору, если их точная сумма не указана в документе. Согласно ст. 809 ГК РФ, в этом случае, нужно исходить из ключевой ставки ЦБ РФ. На 02. 05. 2020 года она установлена в размере 9,25% годовых.

Для наглядности расчёта стоит привести несколько примеров:

Был выдан займ на сумму 150 000 рублей на 3 месяца	сумма процентов к уплате за год: 150 000 * 9,25% = 13 875 рублей.Сумма процентов к уплате за месяц пользования средствами: 13 875 / 12 = 1 156,25 рублей. Сумма процентов к уплате за 3 месяца: 1 156,25 * 3 = 3 468, 75 рублей. Общая сумма к возврату: 150 000 + 3 468, 75 = 153 468, 75 рублей
Был выдан займ на сумму 20 000 рублей под 1,5% в день на 17 дней	сумма процентов к уплате за день пользования средствами: 20 000 * 1,5% = 300 рублей.Сумма процентов за весь период заимствования: 300 * 17 = 5 100 рублей. Сумма к возврату: 20 000 + 5 100 = 25 100 рублей.

Точно также считаются проценты за просрочку по займу.

Простой и сложный процент, в чем отличие

В математике один процент – одна сотая часть числа. Говоря о банковском проценте, обычно подразумевают сумму денег, начисленную по определенным правилам и скопившуюся к конкретному сроку.

Все условия начисления процентов обязательно указываются в договоре между сторонами. Имеют значение такие факторы:

• размер годовой процентной ставки,
• капитализация процентов,
• срок договора,
• порядок выплаты процентов.

Кроме размера ставки, т.е количества начисленных за год процентов, на конечную сумму существенно влияет наличие или отсутствие по условиям договора капитализации процентов.

Это приводит к тому, что один и тот же процент, начисленный в первый период, всегда меньше, чем в последующий – ведь база для исчисления процента вырастает со временем. Такой процент называется сложным процентом.

Во вкладах и кредитах, где база для начисления процента не меняется со временем, всегда остается равной первоначальной сумме, расчет производится по формуле простых процентов.

Как использовать банковский калькулятор

Большинство банков имеют на своем сайте банковский калькулятор, который определяет процентную ставку, а также переводит ее в денежный эквивалент. С такой функцией сайта просчет процентной ставки по кредиту займет несколько минут. Банковская программа может учитывать дополнительные параметры, увеличивая или снижая стоимость кредитной программы.

Например, для действующих клиентов условия кредитования пересчитываются в лучшую сторону. А вот заемщикам с плохой кредитной историей придется заплатить больше, чем требуют стандартные условия банка. Такой перерасчет обусловлен некой подстраховкой кредита в случае работы с недобросовестными клиентами.

Также существуют калькуляторы, которые сравнивают ставку в год сразу нескольких кредиторов. Это очень удобно, если заемщик выбирает из нескольких вариантов. Такой просчет позволяет найти оптимальное предложение годовой процентной ставки и взять выгодную ссуду.

Определившись с кредитором, лучше еще раз перепроверить все платежи. Сделать это можно как самостоятельно, так и на онлайн-калькуляторе. Не стоит жалеть времени на просчеты, поскольку речь идет о ваших деньгах. Да и крупный кредит берется раз или два в году. Поэтому лучше найти какие-то нюансы сразу, чем погашать потом непонятные штрафы и комиссии.

Рассматривая несколько кредитных предложений, стоит внимательно проверить размер ежемесячных платежей. Это позволит избежать скрытых доплат, а также полностью погасить долг в указанные сроки!